AES加密
AES加密是一种对称加密算法,全称为Advanced Encryption Standard,高级加密标准,在密码学中又称Rijndael加密法。它是一种区块加密标准,目前是最流行的一种对称加密算法。该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计,结合两位作者的名字,以Rijndael为名投稿高级加密标准的甄选流程。
AES加密流程很简单,整体过程可以用下面这张图表示(点击可查看大图):
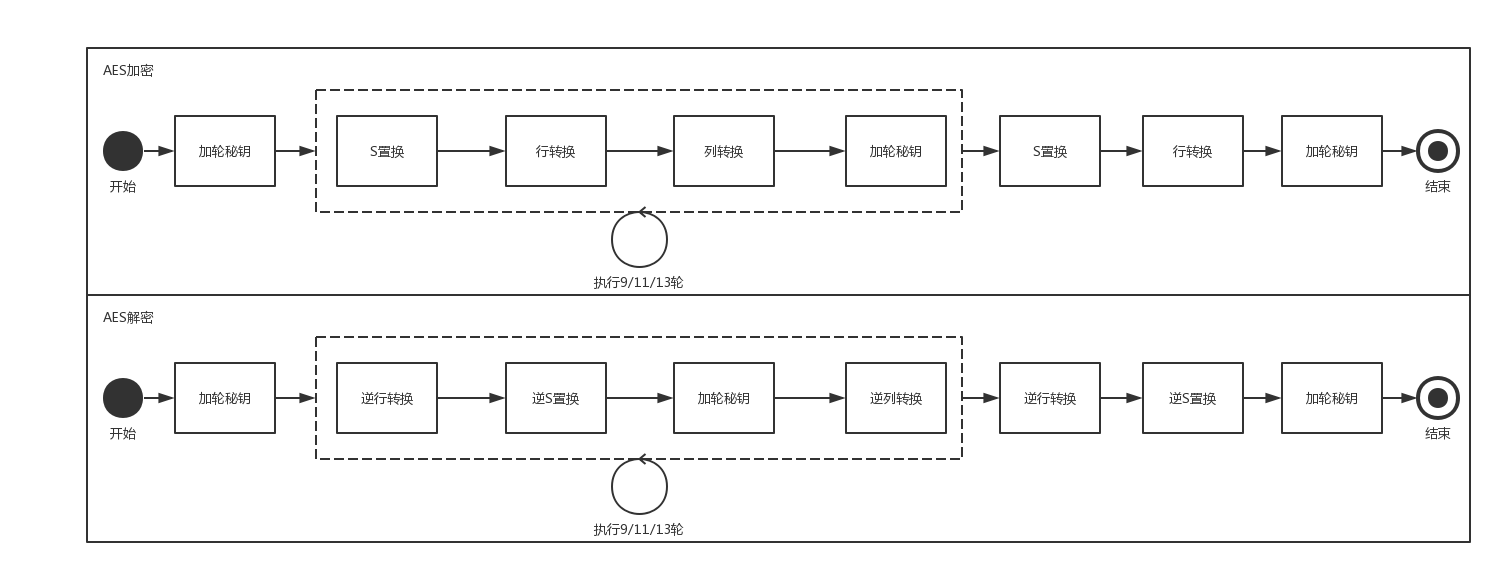
其中,中间的9/11/13轮分别是在秘钥长度为128bits、192bits和256bits时使用的轮数。
图片上很多步骤如果不了解肯定是一脸懵逼,这些步骤都是在AES中定义好的一些操作,后面分开来讲一下每一步都要干嘛。
在开始了解AES之前,我们先来了解一些基本的数学知识(没错,又是数学知识)。
在关键算法领域数学依旧占有举足轻重的地位。
伽罗华域
伽罗华域是包含有限个元素的域,也叫做有限域,最常见的有限域是对素数取模组成的一个集合,然后域中的四则运算与普通集合无异,只是结果要对域定义时的质数取模。
域中有两个重要概念,一个是加法逆元,一个是乘法逆元,加法逆元定义就是两数相加结果为\(0\),乘法逆元则是两数相乘结果为\(1\)。乘法逆元的意义很重要,因为除法本质上与乘逆没有区别,举个例子:10进制下\(8\)的乘法逆元为\(\frac{1}{8}\),则有下面的等式成立:\(32 \div 8 = 32 \times \frac{1}{8} = 4\)。逆元是除法是否可计算的关键。
在密码领域中用的最多的则是以\(2^m\)为底的域,通常这个域计作\(GF(2^m)\),这个域有一个特点,比如\(GF(2^4)\),域中的元素为\(\{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}\),刚好对应16进制的0~F,换句话说\(GF(2^m)\)中的\(m\)可以与计算机中的bit位数对应起来,就比如\(GF(2^8)\)可以与一个字节的数据的所有形式形成对应。
\(GF(2^8)\)在定义运算中,加减法使用异或代替,不难看出所有结果依旧还在定义内,但是在定义乘法里面遇到了问题,那就是乘法中取模的时候,由于会存在公约数\(2\)的倍数的情况,导致一些元素不存在乘法逆元,举个例子:在\(GF(2^4)\)中考察\(2\)的倍数,结果为:\(0,2,4,6,8,10,12,14,0,2,4,6,8,10,12,14\),找不到乘法逆元,也就是说一个数除以\(2\)在某些情况下会造成无法计算的囧境。为解决这个问题,数学家们引入了不可约多项式概念。
可能到这儿你有点迷茫,这怎么又扯到多项式去了。这里具体为啥域内的元素可以转化为多项式,估计你得问问数学家们这么做有什么好处了。现阶段\(GF(2^8)\)域中元素可以这样转化为多项式,比如\(GF(2^8)\)中元素\(113\)使用2进制表示为\(01110001_{(2)}\),数学家们发明了一种神奇的记法来记这个数字:\(x^6+x^5+x^4+0\times x^3+0\times x^2+0\times x^1+x^0=x^6+x^5+x^4+1\)。
这就是这个数字的多项式记法,至于原因暂且没研究过,想研究的话可以去这里https://zh.wikipedia.org/wiki/多项式环。
什么是不可约多项式嘞?简单来说就是没法进一步化简的多项式就叫做不可约多项式。这个东西跟整数范围内的质数概念差不多,至于怎么寻找这个多项式,跟找质数其实差不多,一个一个尝试,看看这个多项式能不能被低次多项式除尽,比如多项式\(x^2-1\)可以被\(x+1\)除尽,因为\(x^2-1=(x+1)(x-1)\)。
所以,要这个不可约多项式有什么用呢?当然有用了!它的作用就是把乘法结果重新归于域范围内,并且使所有的元素存在逆元。
具体是这么使用的(取不可约多项式为0x11B即\(100011011_{(2)}\)):
$$
\begin{align}
10000000_{(2)}\times 00000100_{(2)} &= x^{7}\times x^{2} \\
&= x^{8}\times x \\
&= (x^{8} + 100011011_{(2)})\times x \\
&= (x^{8} + x^{8} + x^{4} + x^{3} + x + 1)\times x \\
&= (x^{4} + x^{3} + x + 1)\times x \\
&= x^{5} + x^{4} + x^{2} + x \\
&= 00110110_{(2)}
\end{align}
$$
也就是在结果溢出域范围的时候使用不可约多项式与结果进行异或运算,让结果重新回到域范围内。
好了,了解了不可约多项式,下面我要直接上结论了:\(GF(2^8)\)中所有的不可约多项式为:
0x11B,0x11D,0x12B,0x12D,0x139,0x13F,0x14D,0x15F,
0x163,0x165,0x169,0x171,0x177,0x17B,0x187,0x18B,
0x18D,0x19F,0x1A3,0x1A9,0x1B1,0x1BD,0x1C3,0x1CF,
0x1D7,0x1DD,0x1E7,0x1F3,0x1F5,0x1F9
得到这些数字的方法其实也很简单,遍历0x100~0x1FF,看看哪些可以满足作为乘法的不可约多项式可以让所有元素逆元存在,以上是程序遍历的结果。
哈?为啥不要超过0x1FF的结果?emmmmmmmmm……举个例子:0x111B,溢出异或时会把结果异或为0x10xx,或许你可以忽略最高的那个1,那这样的话它跟0x11B有什么区别呢?对吧?还有比如0x21B,这个连最高位的1都异或不掉,还会添一个1进去,变成0x3xx……所以只需要考察0x100~0x1FF。
其实主要是看后面一个字节的数字,前面取0x100只是为了方便溢出时剔除高位的1,并没有其他作用。
OK,到这里伽罗华域介绍基本完毕。
需要注意的是算乘法的时候要在溢出处处理,而不是先算一个超出很大范围的结果再异或回来。也就是说,每次都要把作为乘数的多项式每一项拆出来,并且每次与被乘数相乘的时候只能乘\(1\)或者\(x\),处理完之后发现溢出就要与不可约多项式异或,将结果纠正回来。
矩阵
AES加密中运用到大量矩阵计算。
矩阵的概念就不再赘述了,这里主要复习一下矩阵求逆的运算。
矩阵求逆算法其实不难,只是大学时代的知识可能会有很多人忘掉,但是AES的解密运算中需要对列转换操作使用到的矩阵求逆,所以还是有必要了解一下的。
算法简述:
- 为当前矩阵并列一个伴随矩阵(大小相同的单位矩阵),把第一列选为当前要归0的列,第一行选为当前行;
- 把当前列不为0的行与当前行进行行交换;
- 把当前要归0的列上向下不是0的数全部变为1;
- 使用行运算,向下把除当前行以外的其他行当前位置归为0;
- 选择当前行下一行为当前行,当前列的下一列为当前列,回到第二步,直到选到矩阵最后一列;
- 选择最后一行为当前行;
- 通过当前行,把其他行对应列变为0;
- 选取当前行上一行为当前行,重复第七步,直到左边变为伴随矩阵。
这样处理完之后,左侧变成了一个单位矩阵,右侧伴随矩阵就是所求矩阵的逆。
举例,在\(GF(2^8)\)对下面的矩阵进行求逆:
$$
\begin{matrix}
2 & 3 & 1 & 1 \\
1 & 2 & 3 & 1 \\
1 & 1 & 2 & 3 \\
3 & 1 & 1 & 2
\end{matrix}
$$
伴随矩阵:
$$
\begin{matrix}
2 & 3 & 1 & 1 & | & 1 & 0 & 0 & 0 \\
1 & 2 & 3 & 1 & | & 0 & 1 & 0 & 0 \\
1 & 1 & 2 & 3 & | & 0 & 0 & 1 & 0 \\
3 & 1 & 1 & 2 & | & 0 & 0 & 0 & 1
\end{matrix}
$$
将第一列全部变为1:
$$
\begin{matrix}
1 & 8C & 8D & 8D & | & 8D & 0 & 0 & 0 \\
1 & 2 & 3 & 1 & | & 0 & 1 & 0 & 0 \\
1 & 1 & 2 & 3 & | & 0 & 0 & 1 & 0 \\
1 & F6 & F6 & F7 & | & 0 & 0 & 0 & F6
\end{matrix}
$$
使用第一行与其它行进行行计算,把第一列除了第一行,其他全部变为0:
$$
\begin{matrix}
1 & 8C & 8D & 8D & | & 8D & 0 & 0 & 0 \\
0 & 8E & 8E & 8C & | & 8D & 1 & 0 & 0 \\
0 & 8D & 8F & 8E & | & 8D & 0 & 1 & 0 \\
0 & 7A & 7B & 7A & | & 8D & 0 & 0 & F6
\end{matrix}
$$
继续按照这个方法处理其它行:
$$
\begin{matrix}
1 & 8C & 8D & 8D & | & 8D & 0 & 0 & 0 \\
0 & 1 & 1 & 68 & | & D1 & B9 & 0 & 0 \\
0 & 0 & 1 & 5D & | & 34 & E5 & 8D & 0 \\
0 & 0 & 0 & 1 & | & B & D & 9 & E
\end{matrix}
$$
通过当前行,把其他行对应列变为0:
$$
\begin{matrix}
1 & 8C & 8D & 0 & | & 5 & 8B & 89 & 7 \\
0 & 1 & 1 & 0 & | & 4 & 7 & 5 & 6 \\
0 & 0 & 1 & 0 & | & D & 9 & E & B \\
0 & 0 & 0 & 1 & | & B & D & 9 & E
\end{matrix}
$$
把左边化为单位矩阵:
$$
\begin{matrix}
1 & 0 & 0 & 0 & | & E & B & D & 9 \\
0 & 1 & 0 & 0 & | & 9 & E & B & D \\
0 & 0 & 1 & 0 & | & D & 9 & E & B \\
0 & 0 & 0 & 1 & | & B & D & 9 & E
\end{matrix}
$$
右侧就是我们要的结果。
emmmmmmm,到这里,准备知识就差不多了,接下来我们来看AES加密到底是个什么玩意吧:
AES加密中的各项操作
首先说明,AES加密流程中发生的运算全部都在\(GF(2^8)\)下,后面的运算不再特殊说明!
行转换
从简单的说起,行转换比较容易,他的操作图示如下:
$$
\begin{matrix}
\begin{matrix}
1 & 5 & 9 & 13 \\
2 & 6 & 10 & 14 \\
3 & 7 & 11 & 15 \\
4 & 8 & 12 & 16
\end{matrix}
&
\Rightarrow
&
\begin{matrix}
1 & 5 & 9 & 13 \\
6 & 10 & 14 & 2 \\
11 & 15 & 3 & 7 \\
16 & 4 & 8 & 12
\end{matrix}
\end{matrix}
$$
左侧为原数据,每一格表示一个字节,右侧为行转换之后的数据,与原先的标号一一对应。
列转换
列转换操作也很简单,另下面的矩阵与数据中的每一列相乘,把所得的结果替换到那个列即可。
$$
\begin{matrix}
2 & 3 & 1 & 1 \\
1 & 2 & 3 & 1 \\
1 & 1 & 2 & 3 \\
3 & 1 & 1 & 2
\end{matrix}
$$
可以用下面这个式子验证结果:
$$
\begin{matrix}
\begin{matrix}
2 & 3 & 1 & 1 \\
1 & 2 & 3 & 1 \\
1 & 1 & 2 & 3 \\
3 & 1 & 1 & 2
\end{matrix}
&
\times
&
\begin{matrix}
D4 \\
BF \\
5D \\
30
\end{matrix}
&
=
&
\begin{matrix}
04 \\
66 \\
81 \\
E5
\end{matrix}
\end{matrix}
$$
S置换
这个操作其实也没那么难,只是通过SBox替换数据中的每一个字节。
SBox是一个\(16\times 16\)的矩阵,它在不可约多项式取0x11B并且仿射变换为基本定义的话长这个样子:
SBox in Trans_C = 0x63, TransCube(5), GF28Root = 0x11B is
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76,
1 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0,
2 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15,
3 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75,
4 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84,
5 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf,
6 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8,
7 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2,
8 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73,
9 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb,
A 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79,
B 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08,
C 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a,
D 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e,
E 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf,
F 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16
如何使用它呢?举个例子:数据中取到一个字节为0x2F,查SBox,第2行第F列值为:0x15,所以就把0x2F替换为0x15,就这么简单。
估计有人会好奇,这SBox是怎么生成的?
这里查了一下资料,最后得知SBox是通过以下过程得到的:
先对\(GF(2^8)\)下的每一个元素求逆,组建一个\(16\times 16\)的矩阵,然后取每一个元素进行下面的计算:
$$
\begin{matrix}
\begin{matrix}
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\
0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \\
1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\
1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 1
\end{matrix}
&
\times
&
X
&
+
&
C
&
=
&
Y
\end{matrix}
$$
其中\(X\)为元素二进制值的单列矩阵,比如0x2A就是\([00101010]^T\),\(C\)一般取\([01100011]^T\)(即0x63),\(Y\)为结果,把\(Y\)表示的数据替换为当前元素。
加轮秘钥
轮秘钥其实就是所给的秘钥经过固定轮数变化后的当前轮使用的秘钥。
加轮秘钥就是把数据与当前轮使用的秘钥相加。
第一轮中用到的秘钥自然就是秘钥本身。
第二轮秘钥需要做如下变化:
假设初始秘钥表示为\([R_1,R_2,R_3,R_4]\),其中\(R_1,R_2,R_3,R_4\)分别表示秘钥的四个列。
取秘钥第四列\(R_4\),进行如下操作:
$$
\begin{matrix}
\begin{matrix}
1 \\
2 \\
3 \\
4
\end{matrix}
&
\Rightarrow
&
\begin{matrix}
2 \\
3 \\
4 \\
1
\end{matrix}
&
\begin{matrix}
S置换 \\
\rightarrow
\end{matrix}
&
\begin{matrix}
2’ \\
3’ \\
4’ \\
1’
\end{matrix}
\end{matrix}
$$
然后通过如下步骤计算新的\(R_1\)(计作\(R_1’\)):
$$
\begin{matrix}
&
R_1’
&
=
&
R_1
&
+
&
\begin{matrix}
2’ \\
3’ \\
4’ \\
1’
\end{matrix}
&
+
&
RCon_1
\end{matrix}
$$
然后后面的列计算就简单了:
$$
R_2’ = R_2 + R_1’ \\
R_3’ = R_3 + R_2’ \\
R_4’ = R_4 + R_3’
$$
然后\([R_1’,R_2’,R_3’,R_4’]\)组成第二轮的轮秘钥。
后面每轮都按照这个操作处理,初始秘钥为上次一轮的秘钥,\(RCon_1\)换成对应的\(RCon_i\)。
这里用到了一个东西叫做\(RCon_i\),这个东西其实变化很简单。
$$
RCon_1=[1,0,0,0]^T,RCon_i=RCon_{i-1}\times 2\;(i>1)
$$
注意\(GF(2^8)\)运算规则。
以上就是AES加密的所有内容了。
解密
解密就是把加密的流程反过来,全部都反,注意SBox要反,列变换中的矩阵要求逆(不知道为啥请自觉复习矩阵基础知识),轮秘钥要从最后一个倒着来,流程是一样哒。
写在最后
从整篇文章可以看出,AES加密其实就是定义好的一系列流程。
注意AES加密是以16字节的块为单位对数据进行处理的,如果数据最后几字节不符合块要求需要补齐。
秘钥可以使用128bit,192bit和256bit版本,多出来的那几列怎么处理呢?其实AES里面秘钥不是看成一个整体,而是看成一束流,比如192bit秘钥其实就是24字节,也就是\([R_1,R_2,R_3,R_4,R_5,R_6]\),当前四列用完之后,直接使用轮秘钥变换操作向后填充,第二轮的时候其实使用的是\([R_5,R_6,R_1’,R_2’]\)。
影响AES加密流程中数据的有如下因素:\(GF(2^8)\)不可约多项式的选择,RCon的定义(间接受\(GF(2^8)\)域不可约多项式的选择的影响)和轮秘钥变换方法,SBox生成时仿射变换的定义(\(C\)和那个变换矩阵都可以自定义),列变换时所用的矩阵,行变换方法定义。任何一个小环节都可以影响加解密流程的结果,但是这样修改之后到底还是不是AES不好说。但是有一点:操作必须可反,否则解不开。
那么AES安全吗?
以下节选自Wikipedia:
截至2006年,针对AES唯一的成功攻击是旁道攻击。美国国家安全局审核了所有的参与竞选AES的最终入围者(包括Rijndael),认为他们均能够满足美国政府传递非机密文件的安全需要。2003年6月,美国政府宣布AES可以用于加密机密文件:
The design and strength of all key lengths of the AES algorithm(i.e., 128, 192 and 256)are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use.
(译:AES加密算法(使用128,192,和256比特密钥的版本)的安全性,在设计结构及密钥的长度上俱已到达保护机密信息的标准。最高机密信息的传递,则至少需要192或256比特的密钥长度。用以传递国家安全信息的AES实现产品,必须先由国家安全局审核认证,方能被发放使用。)
这标志着,由美国国家安全局NSA批准在最高机密信息上使用的加密系统首次可以被公开使用。许多大众化产品只使用128位密钥当作默认值;由于最高机密文件的加密系统必须保证数十年以上的安全性,故推测NSA可能认为128位太短,才以更长的密钥长度为最高机密的加密保留了安全空间。
通常破解一个区块加密系统最常见的方式,是先对其较弱版本(加密循环次数较少)尝试各种攻击。AES中128位密钥版本有10个加密循环,192比特密钥版本有12个加密循环,256比特密钥版本则有14个加密循环。至2006年为止,最著名的攻击是针对AES 7次加密循环的128位密钥版本,8次加密循环的192比特密钥版本,和9次加密循环的256比特密钥版本所作的攻击。
由于已遭破解的弱版的AES,其加密循环数和原本的加密循环数相差无几,有些密码学家开始担心AES的安全性:要是有人能将该著名的攻击加以改进,这个区块加密系统就会被破解。在密码学的意义上,只要存在一个方法,比穷举法还要更有效率,就能被视为一种“破解”。故一个针对AES 128位密钥的攻击若“只”需要\(2^{120}\)计算复杂度(少于穷举法\(2^{128}\)),128位密钥的AES就算被破解了;即便该方法在目前还不实用。从应用的角度来看,这种程度的破解依然太不切实际。最著名的暴力攻击法是distributed.net针对64位密钥RC5所作的攻击。(该攻击在2002年完成。根据摩尔定律,到2005年12月,同样的攻击应该可以破解66比特密钥的RC5。)
其他的争议则着重于AES的数学结构。不像其他区块加密系统,AES具有相当井然有序的代数结构。虽然相关的代数攻击尚未出现,但有许多学者认为,把安全性创建于未经透彻研究过的结构上是有风险的。Ferguson,Schroeppel和Whiting因此写道:“…我们很担心Rijndael(AES)算法应用在机密系统上的安全性。”
2002年,Nicolas Courtois和Josef Pieprzyk发表名为XSL攻击的理论性攻击,试图展示AES一个潜在的弱点。但几位密码学专家发现该攻击的数学分析有点问题,推测应是作者的计算有误。因此,这种攻击法是否对AES奏效,仍是未解之谜。就现阶段而言,XSL攻击AES的效果不十分显著,故将之应用于实际情况的可能性并不高。
简单总结一下这段描述就是:现阶段,没有行之有效的破解AES加密的方法,但是也没有人能证明AES加密绝对安全,当轮数少于9轮时是相对不安全的,当前的AES加密一般都选择长一点的秘钥和尽可能多的轮数。
总结下来……等于没说……
但是加密算法的可靠性有时候并不是单单看方法的,比如加密时使用的模式:ECB、CBC、OFB、CTR等,可参考这边博客AES五种加密模式。简单来说,工具大家都有,但是用得好不好,不在于工具,而在于使用者的水平。
现阶段一般采用的模式是秘钥使用RSA加密,然后数据使用AES这种速度快安全性好的对称加密。
AES加密作为现阶段使用度最广的加密算法是很值得好好研究的,实现中的关键的关键是实现\(GF(2^8)\)中的所有性质。
AES加密到此结束。
结语
今天更新一下这个鸽了快一周的文章……
前一段时间其实我是在思考这个文章要不要更新,AES加密这个东西其实要讲的不多,而且连续好几篇高难度的文章,后面更新一篇很没技术含量的文章会显得很突兀……
不过最后我还是决定把它更了吧,标题都放上了,不更新说不过去。
附录
AES加密在普通情况下的一些常定义
SBox:
/* S_Box in Trans_C = 0x63, TransCube(5), GF28Root = 0x1B is
* 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76,
* 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0,
* 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15,
* 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75,
* 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84,
* 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf,
* 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8,
* 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2,
* 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73,
* 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb,
* 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79,
* 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08,
* 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a,
* 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e,
* 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf,
* 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16
*/
解密用SBox:
/* S_Box_Reverse in Trans_C = 0x63, TransCube(5), GF28Root = 0x1B is
* 0x52,0x09,0x6a,0xd5,0x30,0x36,0xa5,0x38,0xbf,0x40,0xa3,0x9e,0x81,0xf3,0xd7,0xfb,
* 0x7c,0xe3,0x39,0x82,0x9b,0x2f,0xff,0x87,0x34,0x8e,0x43,0x44,0xc4,0xde,0xe9,0xcb,
* 0x54,0x7b,0x94,0x32,0xa6,0xc2,0x23,0x3d,0xee,0x4c,0x95,0x0b,0x42,0xfa,0xc3,0x4e,
* 0x08,0x2e,0xa1,0x66,0x28,0xd9,0x24,0xb2,0x76,0x5b,0xa2,0x49,0x6d,0x8b,0xd1,0x25,
* 0x72,0xf8,0xf6,0x64,0x86,0x68,0x98,0x16,0xd4,0xa4,0x5c,0xcc,0x5d,0x65,0xb6,0x92,
* 0x6c,0x70,0x48,0x50,0xfd,0xed,0xb9,0xda,0x5e,0x15,0x46,0x57,0xa7,0x8d,0x9d,0x84,
* 0x90,0xd8,0xab,0x00,0x8c,0xbc,0xd3,0x0a,0xf7,0xe4,0x58,0x05,0xb8,0xb3,0x45,0x06,
* 0xd0,0x2c,0x1e,0x8f,0xca,0x3f,0x0f,0x02,0xc1,0xaf,0xbd,0x03,0x01,0x13,0x8a,0x6b,
* 0x3a,0x91,0x11,0x41,0x4f,0x67,0xdc,0xea,0x97,0xf2,0xcf,0xce,0xf0,0xb4,0xe6,0x73,
* 0x96,0xac,0x74,0x22,0xe7,0xad,0x35,0x85,0xe2,0xf9,0x37,0xe8,0x1c,0x75,0xdf,0x6e,
* 0x47,0xf1,0x1a,0x71,0x1d,0x29,0xc5,0x89,0x6f,0xb7,0x62,0x0e,0xaa,0x18,0xbe,0x1b,
* 0xfc,0x56,0x3e,0x4b,0xc6,0xd2,0x79,0x20,0x9a,0xdb,0xc0,0xfe,0x78,0xcd,0x5a,0xf4,
* 0x1f,0xdd,0xa8,0x33,0x88,0x07,0xc7,0x31,0xb1,0x12,0x10,0x59,0x27,0x80,0xec,0x5f,
* 0x60,0x51,0x7f,0xa9,0x19,0xb5,0x4a,0x0d,0x2d,0xe5,0x7a,0x9f,0x93,0xc9,0x9c,0xef,
* 0xa0,0xe0,0x3b,0x4d,0xae,0x2a,0xf5,0xb0,0xc8,0xeb,0xbb,0x3c,0x83,0x53,0x99,0x61,
* 0x17,0x2b,0x04,0x7e,0xba,0x77,0xd6,0x26,0xe1,0x69,0x14,0x63,0x55,0x21,0x0c,0x7d
*/
解密用列变换矩阵:
/* Column_Trans_Cube_Reverse should be
* 0E, 0B, 0D, 09;
* 09, 0E, 0B, 0D;
* 0D, 09, 0E, 0B;
* 0B, 0D, 09, 0E
*/